Nptel Deep Learning - IIT Ropar Week 1 Assignment Answer

ABOUT THE COURSE :
Deep Learning has received a lot of attention over the past few years and has been employed successfully by companies like Google, Microsoft, IBM, Facebook, Twitter etc. to solve a wide range of problems in Computer Vision and Natural Language Processing. In this course we will learn about the building blocks used in these Deep Learning based solutions. Specifically, we will learn about feedforward neural networks, convolutional neural networks, recurrent neural networks and attention mechanisms. We will also look at various optimization algorithms such as Gradient Descent, Nesterov Accelerated Gradient Descent, Adam, AdaGrad and RMSProp which are used for training such deep neural networks. At the end of this course students would have knowledge of deep architectures used for solving various Vision and NLP tasks

INTENDED AUDIENCE: Any Interested Learners

PREREQUISITES: Working knowledge of Linear Algebra, Probability Theory. It would be beneficial if the participants have done a course on Machine Learning.

Nptel Deep Learning – IIT Ropar Week 1 Assignment Answer

Course layout

Week 1 : (Partial) History of Deep Learning, Deep Learning Success Stories, McCulloch Pitts Neuron, Thresholding Logic, Perceptrons, Perceptron Learning Algorithm

Week 2 : Multilayer Perceptrons (MLPs), Representation Power of MLPs, Sigmoid Neurons, Gradient Descent, Feedforward Neural Networks, Representation Power of Feedforward Neural Networks

Week 3 : FeedForward Neural Networks, Backpropagation

Week 4 : Gradient Descent (GD), Momentum Based GD, Nesterov Accelerated GD, Stochastic GD, AdaGrad, RMSProp, Adam, Eigenvalues and eigenvectors, Eigenvalue Decomposition, Basis

Week 5 : Principal Component Analysis and its interpretations, Singular Value Decomposition

Week 6 : Autoencoders and relation to PCA, Regularization in autoencoders, Denoising autoencoders, Sparse autoencoders, Contractive autoencoders

Week 7 : Regularization: Bias Variance Tradeoff, L2 regularization, Early stopping, Dataset augmentation, Parameter sharing and tying, Injecting noise at input, Ensemble methods, Dropout

Week 8 : Greedy Layerwise Pre-training, Better activation functions, Better weight initialization methods, Batch Normalization

Week 9 : Learning Vectorial Representations Of Words

Week 10: Convolutional Neural Networks, LeNet, AlexNet, ZF-Net, VGGNet, GoogLeNet, ResNet, Visualizing Convolutional Neural Networks, Guided Backpropagation, Deep Dream, Deep Art, Fooling Convolutional Neural Networks

Week 11: Recurrent Neural Networks, Backpropagation through time (BPTT), Vanishing and Exploding Gradients, Truncated BPTT, GRU, LSTMs

Week 12: Encoder Decoder Models, Attention Mechanism, Attention over images

Nptel Deep Learning – IIT Ropar Week 1 Assignment Answer

Week 1 : Assignment 1

Due date: 2025-02-05, 23:59 IST.

Assignment not submitted

Common data for questions 1,2 and 3
In the figure shown below, the blue points belong to class 1 (positive class) and the red points belong to class 0 (negative class). Suppose that we use a perceptron model, with the weight vector w as shown in the figure, to separate these data points. We define the point belongs to class 1 if $w^{T} x \geq 0$

wTx≥0 else it belongs to class 0.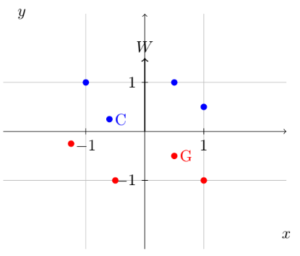

1 point

The points $G$

G and $C$

C will be classified as?
Note: the notation $(G, 0)$

(G,0) denotes the point $G$

G will be classified as class-0 and $(C, 1)$

(C,1) denotes the point $C$

C will be classified as class-1

$(C, 0), (G, 0)$

(C,0),(G,0)

$(C, 0), (G, 1)$

(C,0),(G,1)

$(C, 1), (G, 1)$

(C,1),(G,1)

$(C, 1), (G, 0)$

(C,1),(G,0)

1 point

The statement that “there exists more than one decision lines that could separate these data points with zero error” is,

True

False

1 point

Suppose that we multiply the weight vector w by −1. Then the same points $G$

G and $C$

C will be classified as?

$(C, 0), (G, 0)$

(C,0),(G,0)

$(C, 0), (G, 1)$

(C,0),(G,1)

$(C, 1), (G, 1)$

(C,1),(G,1)

$(C, 1), (G, 0)$

(C,1),(G,0)

1 point

Which of the following can be achieved using the perceptron algorithm in machine learning?

Grouping similar data points into clusters, such as organizing customers based on purchasing behavior.

Solving optimization problems, such as finding the maximum profit in a business scenario.

Classifying data, such as determining whether an email is spam or not.

Finding the shortest path in a graph, such as determining the quickest route between two cities.

1 point

Consider the following table, where $x_{1}$

x1 and $x_{2}$

x2 are features and $y$

y is a label.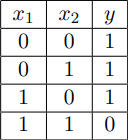

Assume that the elements in w are initialized to zero and the perception learning algorithm is used to update the weights w. If the learning algorithm runs for long enough iterations, then

The algorithm never converges

The algorithm converges (i.e., no further weight updates) after some iterations

The classification error remains greater than zero

The classification error becomes zero eventually

1 point

We know from the lecture that the decision boundary learned by the perceptron is a line in $R^{2}$

R2. We also observed that it divides the entire space of $R^{2}$

R2 into two regions, suppose that the input vector $x \in R^{4}$

x∈R4, then the perceptron decision boundary will divide the whole $R^{4}$

R4 space into how many regions?

It depends on whether the data points are linearly separable or not.

1 point

Choose the correct input-output pair for the given MP Neuron.
$f (x) = {\begin{cases} 1, & if x_{1} + x_{2} + x_{3} < 2 \\ 0, & otherwise \end{cases}$

f(x)={1,ifx1+x2+x3<20,otherwise

$y = 1$

y=1 for $(x_{1}, x_{2}, x_{3})$

(x1,x2,x3) = (0, 0, 0)

$y = 0$

y=0 for $(x_{1}, x_{2}, x_{3})$

(x1,x2,x3) = (0, 0, 1)

$y = 1$

y=1 for $(x_{1}, x_{2}, x_{3})$

(x1,x2,x3) = (1, 0, 0)

$y = 1$

y=1 for $(x_{1}, x_{2}, x_{3})$

(x1,x2,x3) = (1, 1, 1)

$y = 0$

y=0 for $(x_{1}, x_{2}, x_{3})$

(x1,x2,x3) = (1, 0, 1)

1 point

Consider the following table, where $x_{1}$

x1 and $x_{2}$

x2 are features (packed into a single vector $x = [\begin{matrix} x_{1} \\ x_{2} \end{matrix}]$

x=[x1x2]) and $y$

y is a label:

Suppose that the perceptron model is used to classify the data points. Suppose further that the weights w are initialized to w = $[\begin{matrix} 1 \\ 1 \end{matrix}]$

[11]. The following rule is used for classification,
$y = {\begin{cases} 1 & if w^{T} x > 0 \\ 0 & if w^{T} x \leq 0 \end{cases}$

y={1ifwTx>00ifwTx≤0

The perceptron learning algorithm is used to update the weight vector w. Then, how many times the weight vector w will get updated during the entire training process?

Not possible to determine

1 point

Which of the following threshold values of MP neuron implements AND Boolean function? Assume that the number of inputs to the neuron is 3 and the neuron does not have any inhibitory inputs.

1 point

Consider points shown in the picture. The vector w = $[\begin{matrix} - 1 \\ 1 \end{matrix}]$

[−11].As per this weight vector, the Perceptron algorithm will predict which classes for the data points $x_{1}$

x1 and $x_{2}$

x2.
NOTE: $y = {\begin{cases} 1 & if w^{T} x > 0 \\ 0 & if w^{T} x \leq 0 \end{cases}$

y={1ifwTx>00ifwTx≤0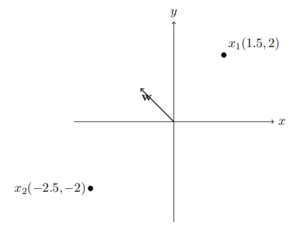

$x_{1}$

x1 = −1

$x_{1}$

x1 = 1

$x_{2}$

x2 = −1

$x_{2}$

x2 = 1

Nptel Deep Learning – IIT Ropar Week 1 Assignment Answer

Nptel Deep Learning – IIT Ropar Week 1 Assignment Answer

Course layout

Nptel Deep Learning – IIT Ropar Week 1 Assignment Answer

Week 1 : Assignment 1

Related Posts

Nptel Deep Learning – IIT Ropar Week 3 Assignment Answer

Nptel Deep Learning – IIT Ropar Week 2 Assignment Answer

Leave a Reply